Grid Paths Problem
and Dynamic Programming Solution to it using memoization and tabulation in Rust Language.
Introduction
Grid Paths is another Dynamic Problem based on grids.
In this problem, you are given a grid with traps / obstacles. You have to tell the number of unique paths to reach from top left to bottom right in the grid, without stepping onto trap.
You can only move in right and down directions.
This problem is taken from CSES Problem Set
In the grid, . denotes an empty cell, and * denotes a trap.
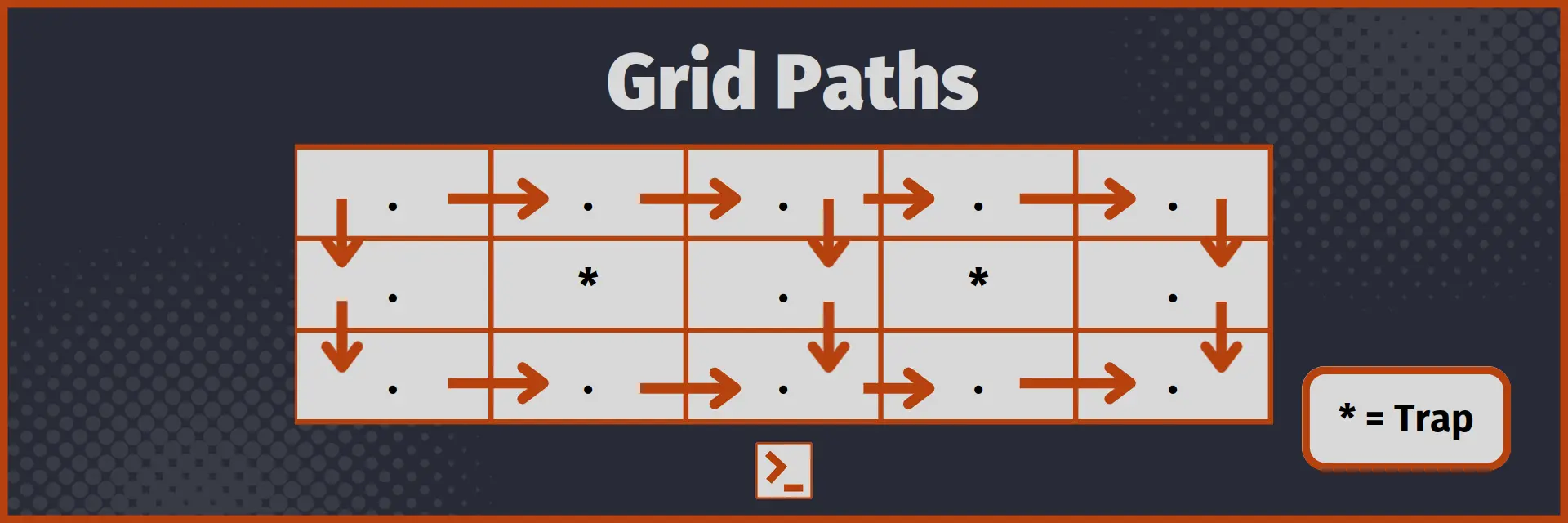
So, for above grid, answer is 3
Recursive Solution
In recursive solution, we start from the end, that is, bottom right cell, and take sum of paths of cell upwards and leftwards to it.
If the cell is * in the grid, we return 0.
Algorithm
- If the value of cell in grid is
*, return 0. - Base Case would be that, if the current grid has 1 column and 1 row, return 1.
- If current Grid has 1 row, we can traverse only leftwards. So, return Grid Paths of the left cell.
- Similarly, If current Grid has 1 column, we can traverse only upwards. So, return Grid Paths of the upper cell.
- Else, return the sum of Grid Paths of left and upper cells.
Function
Here is the function using above algorithm
fn grid_paths(grid:&Vec<Vec<char>>, r:usize, c:usize) -> usize{// If there is no row or column in the grid, return 0if r<1 || c < 1 { return 0; }// If corresponding grid value is *, return 0if grid[r-1][c-1] == '*' { return 0;}// Base Case// If only 1 row and column, return 1if r == 1 && c==1 { return 1; }// Recursive Cases// If only 1 row, can go only leftif r == 1 { return grid_paths(grid, 1, c-1); }// If only 1 column, can go only upif c == 1 { return grid_paths(grid, r-1, 1); }// Else, return sum of upper and left valuesreturn grid_paths(grid, r-1, c) + grid_paths(grid, r, c-1);}
With Driver code
fn grid_paths(grid:&Vec<Vec<char>>, r:usize, c:usize) -> usize{// If there is no row or column in the grid, return 0if r<1 || c < 1 { return 0; }// If corresponding grid value is *, return 0if grid[r-1][c-1] == '*' { return 0;}// Base Case// If only 1 row and column, return 1if r == 1 && c==1 { return 1; }// Recursive Cases// If only 1 row, can go only leftif r == 1 { return grid_paths(grid, 1, c-1); }// If only 1 column, can go only upif c == 1 { return grid_paths(grid, r-1, 1); }// Else, return sum of upper and left valuesreturn grid_paths(grid, r-1, c) + grid_paths(grid, r, c-1);}// Driver Codefn main() {// Take the sample grid, as shown in picturelet grid = vec![vec!['.', '.', '.', '.', '.'],vec!['.', '*', '.', '*', '.'],vec!['.', '.', '.', '.', '.'],];// Print The number of paths of the gridprintln!("{}", grid_paths(&grid, grid.len(), grid[0].len()));}
Output
3
Time Complexity : O( 2r+c )
Space Complexity : O( r+c )
( Space complexity includes recursive stack space )
Overlapping Sub-problems
If we have a look carefully on recursive approach, we computed multiple results many times.
For example : In a 20×20 grid, you can reach the (10, 10) cell in thousands of ways, and takes thousands of recursions each time to calculate.
These are called Overlapping Sub-problems because they are smaller part of large problems, and are computed again and again.
So, we simply calculate them once, and store it in a matrix, and retrieve it when necessary. This helps to save a lot of computation.
This is called Dynamic Programming Approach for the problem.
Memoization ( Top-down DP ) Method
In memoization method, we simply take a DP matrix, and store the computed result.
Algorithm
- Initially, take a DP matrix and set all its elements to
Nonetype. Alternatively, you can set it to -1. - If the grid paths are already calculated, that is given index of matrix is
Someor not -1, return it. - Else, calculate the grid paths by using recursion and store it in the DP matrix.
Function
Here is the function using above algorithm
fn grid_paths(grid:&Vec<Vec<char>>, r:usize, c:usize, dp:&mut Vec<Vec<Option<usize>>>) -> usize{// If there is no row or column in the grid, return 0if r<1 || c < 1 { return 0; }// If already computed, return valueif dp[r-1][c-1].is_some() { return dp[r-1][c-1].unwrap(); }// If corresponding grid value is *, return 0if grid[r-1][c-1] == '*' { dp[r-1][c-1] = Option::from(0); return 0;}// Base Case// If only 1 row and column, return 1if r == 1 && c==1 { dp[0][0] = Option::from(1); return 1; }// Recursive Cases// If only 1 row, can go only leftif r == 1 { dp[0][c-1] = Option::from(grid_paths(grid, 1, c-1, dp)); return dp[0][c-1].unwrap(); }// If only 1 column, can go only upif c == 1 { dp[r-1][0] = Option::from( grid_paths(grid, r-1, 1, dp)); return dp[r-1][0].unwrap(); }// Else, return sum of upper and left valuesdp[r-1][c-1] = Option::from(grid_paths(grid, r-1, c, dp) + grid_paths(grid, r, c-1, dp));return dp[r-1][c-1].unwrap();}
With Driver code
fn grid_paths(grid:&Vec<Vec<char>>, r:usize, c:usize, dp:&mut Vec<Vec<Option<usize>>>) -> usize{// If there is no row or column in the grid, return 0if r<1 || c < 1 { return 0; }// If already computed, return valueif dp[r-1][c-1].is_some() { return dp[r-1][c-1].unwrap(); }// If corresponding grid value is *, return 0if grid[r-1][c-1] == '*' { dp[r-1][c-1] = Option::from(0); return 0;}// Base Case// If only 1 row and column, return 1if r == 1 && c==1 { dp[0][0] = Option::from(1); return 1; }// Recursive Cases// If only 1 row, can go only leftif r == 1 { dp[0][c-1] = Option::from(grid_paths(grid, 1, c-1, dp)); return dp[0][c-1].unwrap(); }// If only 1 column, can go only upif c == 1 { dp[r-1][0] = Option::from( grid_paths(grid, r-1, 1, dp)); return dp[r-1][0].unwrap(); }// Else, return sum of upper and left valuesdp[r-1][c-1] = Option::from(grid_paths(grid, r-1, c, dp) + grid_paths(grid, r, c-1, dp));return dp[r-1][c-1].unwrap();}// Driver Codefn main() {// Take the sample grid, as shown in picturelet grid = vec![vec!['.', '.', '.', '.', '.'],vec!['.', '*', '.', '*', '.'],vec!['.', '.', '.', '.', '.'],];// Initialize DP matrixlet mut dp = vec![vec![None; grid[0].len()]; grid.len()];// Print The number of paths of the gridprintln!("{}", grid_paths(&grid, grid.len(), grid[0].len(), &mut dp));}
Output
3
Time Complexity : O( r*c )
Space Complexity : O( r*c )
Tabulation ( Bottom-up DP ) Method
Although time and space complexities of tabulation as well as memoization method are same, tabulation is much more efficient as there are a lot of expensive recursive calls in memoization.
In tabulation method, we make the DP matrix, and fill it first on the basis of base condition, and then on the basis of previous row.
Algorithm
- Initially, set
1upto first*in first row and column in DP matrix, and 0 after that. - Now, for each of cell, if the corresponding cell in original grid is
*, set it to 0, else sum of upper and left cell in DP matrix. - Finally, return the value of last cell as the answer.
Function
Here is the function using above algorithm
fn grid_paths(grid:&Vec<Vec<char>>, r:usize, c:usize, dp:&mut Vec<Vec<Option<usize>>>) -> usize{// Set the value in the first row upto first * as 1// Trapped variable stores whether * has comelet mut trapped = false;for i in 0..c {if grid[0][i] == '*' { trapped = true; }// If * has already comeif trapped { dp[0][i] = Option::from(0); }else { dp[0][i] = Option::from(1); }}// Set the value in the first column upto first * as 1trapped = false;for i in 0..r {if grid[i][0] == '*' { trapped = true; }// If * has already comeif trapped { dp[i][0] = Option::from(0); }else { dp[i][0] = Option::from(1); }}for i in 1..r {for j in 1..c {// If *, set dp[i][j] = 0if grid[i][j] == '*' { dp[i][j] = Option::from(0); continue; }// Set sum of paths of upper and left celldp[i][j] = Option::from(dp[i-1][j].unwrap() + dp[i][j-1].unwrap() );}}// Return last value as answerreturn dp[r-1][c-1].unwrap();}
Use the same driver code.
Output
3
Time Complexity : O( r*c )
Space Complexity : O( r*c )
Conclusion
Grid Paths is a grid based Dynamic Programming problem.
In this problem, you are given a grid with traps / obstacles. You have to tell the number of unique paths to reach from top left to bottom right in the grid, without stepping onto trap.
You can only move in right and down directions.
In this article, we saw how to solve the Grid Paths problem, first using recursion and then using Dynamic Programming, memoization as well as tabulation method in Rust Language.
Here is the optimized function for easy access
fn grid_paths(grid:&Vec<Vec<char>>, r:usize, c:usize, dp:&mut Vec<Vec<Option<usize>>>) -> usize{let mut trapped = false;for i in 0..c {if grid[0][i] == '*' { trapped = true; }if trapped { dp[0][i] = Option::from(0); } else { dp[0][i] = Option::from(1); } }trapped = false;for i in 0..r {if grid[i][0] == '*' { trapped = true; }if trapped { dp[i][0] = Option::from(0); } else { dp[i][0] = Option::from(1); } }for i in 1..r { for j in 1..c {if grid[i][j] == '*' { dp[i][j] = Option::from(0); continue; }dp[i][j] = Option::from(dp[i-1][j].unwrap() + dp[i][j-1].unwrap() ); } }return dp[r-1][c-1].unwrap();}